Grundlagen

Was ist ein Analogrechner? Viele landläufige Quellen definieren ihn als eine Maschine, die mit kontinuierlichen Größen rechnet, um ihn hiermit von Digitalrechnern abzugrenzen. Diese Unterscheidung ist zwar in der Mehrzahl der Fälle korrekt, es gibt jedoch Ausnahmen in Form digital arbeitender Analogrechner (derartige Maschinen werden als DDA, kurz für "Digital Differential Analyzer", bezeichnet).

Der wirkliche Unterschied zwischen einem Analogrechner und einem (speicherprogrammierten) Digitalrechner liegt in der Struktur der Maschinen begründet. Während ein (speicherprogrammierter) Digitalrechner über eine feste Struktur verfügt, mit deren Hilfe, gesteuert durch einen in Form eines Programmes im Speicher festgelegten Algorithmus, die Lösung sehr unterschiedlicher Problemklassen erlaubt, stellt ein Analogrechner ein System mit einer variablen Struktur dar, das nur für die Behandlung recht eingeschränkter Problemklassen geeignet ist.

Wie ist das zu verstehen? Zunächst einmal besteht ein Analogrechner aus einer mehr oder weniger großen Anzahl einzelner Rechenelemente, mit deren Hilfe grundlegende Operationen wie Integration (!), Summation, Multiplikation, Funktionserzeugung etc. durchgeführt werden können. Diese Rechenelemente können dann - in der Regel mit Hilfe von Steckverbindungen auf einem zentralen Patchfeld - in geeigneter Weise miteinander verbunden werden, um eine bestimmte Funktionalität zu implementieren.

Wie löst man nun ein gegebenes Problem mit Hilfe eines Analogrechners? Zunächst ist festzustellen, dass bestimmte Problemklassen besser als alle anderen für eine Lösung mit Hilfe derartiger Rechner geeignet sind. Hierbei handelt es sich um alle Probleme, die in Form von (gegebenenfalls gekoppelten) Differentialgleichungen in einer Variablen (der Zeit) beschreibbar sind, wozu eine Vielzahl, wenn nicht gar die Mehrzahl technisch/naturwissenschaftlicher Fragestellungen zählt. Hierfür ist das gegebene Problem zunächst mathematisch zu beschreiben, was im Folgenden exemplarisch anhand eines einfachen Masse-Feder-Dämpfer-Systems erfolgen wird:

Welche Elemente sind an einem solchen physikalischen System beteiligt? Offensichtlich eine Masse, eine Feder mit entsprechender Federkonstante und ein Dämpfer. Da es sich um ein abgeschlossenes physikalisches System handelt, muss die Summe der in ihm auftretenden Kräfte gleich Null sein: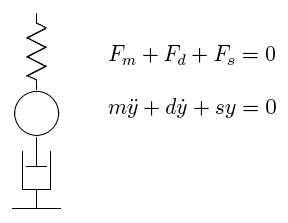

Löst man diese Kräftegleichung nun nach der höchsten auftretenden Ableitung auf, ergibt sich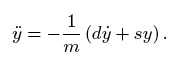

Setzt man nun voraus, dass diese zweite Ableitung bekannt sei, lässt sich mit Hilfe eines Integrierers hieraus zwanglos die nächstniedrigere Ableitung erzeugen (das gedrehte Vorzeichen ist technisch bedingt - nahezu alle Rechenelemente eines elektronischen Analogrechners nehmen eine Vorzeichenvertauschung vor, was zu Anfang mitunter zu Verwirrung führen kann):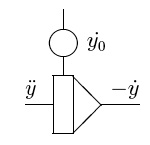

Durch nochmalige Integration kann aus der Geschwindigkeit die Position der Masse erhalten werden: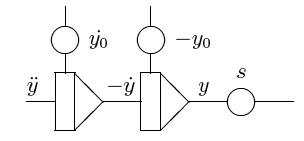

Nachdem nun sy sowie die erste Ableitung von y (mit negativem Vorzeichen) vorliegen, kann nach Bildung des Termes dy' die Summe -(dy' + sy) gebildet werden: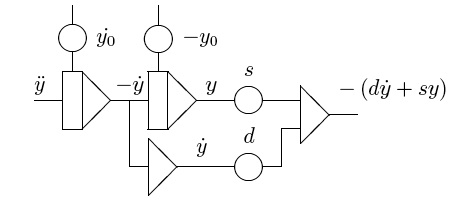

Diese Summe entspricht jedoch - bis auf einen Vorfaktor 1 / m - genau der zu Beginn dieser Überlegungen als bekannt vorausgesetzten zweiten Ableitung von y, d.h. der Beschleunigung der Masse. Auf Basis dieser Erkenntnis kann nun eine Rückführung in die Rechenschaltung eingebaut werden, welche die benötigte Beschleunigung liefert: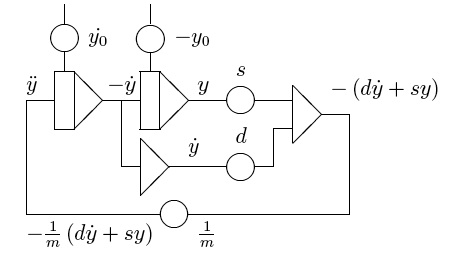

Diese Rechenschaltung kann nun auf dem Steckfeld eines elektronischen Analogrechners implementiert werden. Das folgende Bild zeigt die obige Schaltung umgesetzt auf einem kleinen Telefunken Tischanalogrechner des Typs RA 741:

Dieses einfache Beispiel sollte nur die grundlegende Idee der Programmierung eines Analogrechners demonstrieren: Ausgehend von einer mathematischen Problembeschreibung (in Form gegebenenfalls gekoppelter Differenzialgleichungen) wird eine Rechenschaltung entwickelt, die dann mit Hilfe eines Steckfeldes die Struktur des Analogrechners zur Lösung dieses speziellen Problemes festlegt. Ein solches Vorgehen hat Vor- und Nachteile: Einer der Hauptnachteile ist, dass Analogrechner prinzipbedingt zu einem Zeitpunkt stets der Lösung eines Problemes zugeordnet sind und die Umprogrammierung eines solchen Systems nicht trivial ist. Der Hauptvorteil dieses Vorgehens ist jedoch, dass ein Analogrechner durch den konsequenten Verzicht auf eine speicherbasierte Programmsteuerung bei einer Vielzahl praktischer Probleme traditionellen speicherprogrammierten Digitalrechnern hinsichtlich der erzielbaren Rechenleistung weit überlegen ist! Diese Feststellung gibt Grund zur Hoffnung, dass die Idee des analogen Rechnens vielleicht in nicht allzu ferner Zukunft eine Renaissance erleben wird, wobei sicherlich rein digitale Implementationen der Rechenelemente zum Einsatz gelangen werden.

Eine Vielzahl weiterer Beispiele findet sich auf den Seiten des Analogmuseums beziehungsweise direkt in der dortigen Einleitung beziehungsweise der Sammlung praktischer Beispiele.